Oscillations sur le champ moyen

La transition d'une dynamique statique vers une dynamique non-statique apparaît par une bifurcation de Hopf lorsque l'on augmente le paramètre de gain $g$. Il est important de noter que cette bifurcation intervient sur le système macroscopique (2.6). Cette bifurcation est fondamentalement différente de celle que l'on observe sur les réseaux de taille finie sur le modèle à une population. Avant la bifurcation, les signaux de champ moyen $m^{(1)}(t)$ et $m^{(2)}(t)$ tendent vers les points fixes respectifs ${m^{(1)}}^*$ et ${m^{(2)}}^*$. Après la bifurcation, les signaux de champ moyen $m^{(1)}(t)$ et $m^{(2)}(t)$ décrivent pour les temps longs un cycle périodique ou pseudo-périodique (voir la figure 2.22). La valeur de critique de bifurcation peut être déterminée en observant le rayon spectral de la jacobienne du système (2.6) au point fixe, et en augmentant continûment la valeur de $g$ jusqu'à ce que le rayon spectral dépasse la valeur 1. Pour les paramètres restreints donnés dans l'équation (2.8), tous les régimes synchrones correspondent à de tels cycles. En particulier, on n'observe pas de nouvelles bifurcation de Hopf lorsque l'on augmente $g$, et à plus forte raison on n'observe pas de régime chaotique sur les signaux de champ moyen.

Figure 2.22: Deux exemples de dynamiques cycliques observées sur le signal $m^{(1)}(t)$. Les deux figures du haut montrent un signal périodique de période 5 (Le signal $m^{(1)}(t)$ est sur la gauche, et l'application de premier retour sur la droite). Les paramètres sont $\sigma _J=1$, $d=2$, $g=8$, $\bar{\theta}^{(1)}=0$, $\sigma _\theta ^{(1)}=0$, $\bar{\theta}^{(2)}=0.5$, $\sigma _\theta ^{(2)}=0$. Les deux figures du bas montrent une dynamique pseudo-périodique, dont la période est proche de 5. Les paramètres sont $\sigma _J=1$, $d=2$, $g=8$, $\bar{\theta}^{(1)}=0$, $\sigma _\theta ^{(1)}=0$, $\bar{\theta}^{(2)}=0.8$, $\sigma _\theta ^{(2)}=0.5$.

L'apparition d'un régime synchronisé oscillant dépend essentiellement des paramètres $g$ et $d$. On peut remarquer par ailleurs que le paramètre $\sigma_J$ se comporte qualitativement comme le paramètre $g$. En fixant $\sigma_J$ à 1, et en faisant varier $g$ et $d$, on dresse l'éventail des comportements dynamiques qui peuvent être rencontrés dans notre système.

Le rôle de $g$ comme facteur favorisant la déstabilisation a déjà été étudié dans les sections précédentes, à taille finie et à la limite thermodynamique. On constate également sur ce modèle que des valeurs élevées de $g$ favorisent l'apparition d'oscillations. Néanmoins, le paramètre $d$ joue un rôle tout à fait fondamental dans l'apparition des oscillations. Contrairement à $g$, le paramètre $d$ est caractéristique de ce modèle. Il tend à accentuer le ``contraste'' entre les deux populations. Plus $d$ est élevé, plus les inhibiteurs sont fortement inhibiteurs et plus les excitateurs sont fortement excitateurs. Au contraire, une valeur de $d$ nulle reproduit les paramètres des poids du modèle à une population. $d$ marque donc la différenciation entre les deux populations. On constate sur ce modèle qu'il existe également une valeur de $d$ minimale nécessaire à l'apparition d'oscillations. La présence d'un fort contraste entre les deux populations semble donc une condition nécessaire à l'apparition d'oscillations. Enfin, les paramètres qui portent sur les seuils jouent également un rôle. On a constaté en effet que des oscillations peuvent apparaître à condition que les potentiels de la population inhibitrice soient abaissés par un seuil $\bar{\theta}^{(2)}>0$.

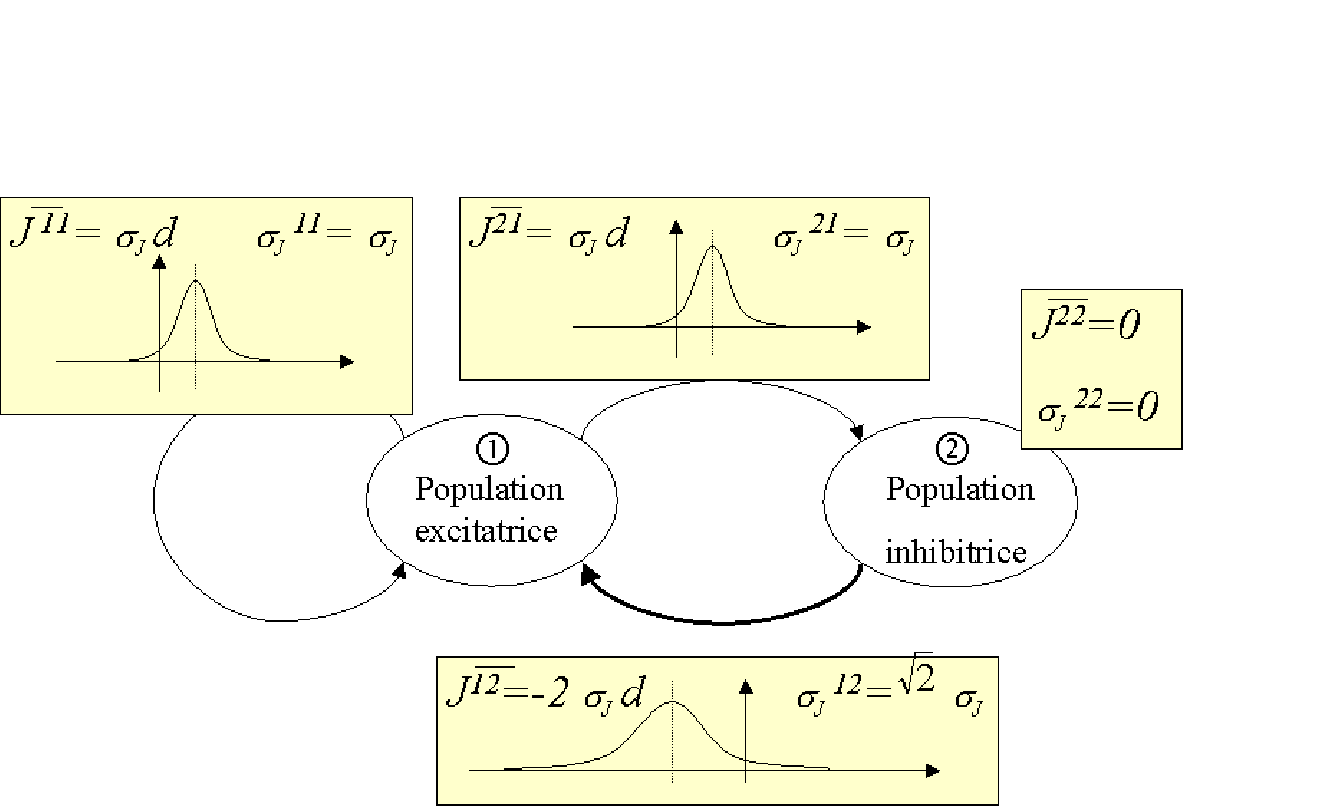
Il est possible de décomposer le mécanisme qui fait apparaître des oscillations dans le système. Dans le modèle (2.8), un fort niveau d'activation sur la population excitatrice conduit grâce aux liens $J_{ij}^{(21)}$ à renforcer le niveau d'activation de la population inhibitrice. La population inhibitrice envoie alors en retour par les liens $J_{ij}^{(12)}$ une influence négative qui tend à abaisser le niveau d'activation de la population excitatrice. Au temps suivant, le niveau d'activation faible sur la population excitatrice ne ``nourrit'' plus la population inhibitrice, qui à son tour voit son niveau d'activation baisser. La population inhibitrice étant désactivée, le niveau d'activation de la population excitatrice se renforce grâce à ses propres liens récurrents.

Ce mécanisme en boucle tend à produire périodiquement un pic d'activation sur la population excitatrice, qui est suivi au temps suivant d'un pic d'activation sur la population inhibitrice. Un décalage de phase peut en effet être observé entre le champ moyen $m^{(1)}(t)$ de la population excitatrice et le champ moyen $m^{(2)}(t)$ de la population inhibitrice ; la synchronisation repose sur un renforcement du niveau d'activation de la population inhibitrice par la population excitatrice (voir la figure 2.23).

On peut remarquer que l'entretien de ce mécanisme nécessite un réglage préalable. Ainsi, si l'influence inhibitrice est trop forte, de telles interactions conduisent à une complète extinction de l'activation de la population excitatrice. Dans le cas contraire, influences inhibitrice et excitatrice se compensent, si bien qu'elles produisent des signaux oscillants. La nécessité d'amoindrir le niveau d'activation de la population inhibitrice justifie la présence du seuil $\bar{\theta}^{(2)}>0$.

De manière plus générale, on peut dire qu'au sein d'une assemblée de neurones, la présence d'une différenciation marquée entre neurones inhibiteurs et neurones excitateurs est une condition nécessaire à l'apparition de régimes synchronisés. Ce point est généralisable à de nombreux types d'ensembles de neurones artificiels, et sans doute vrai la plupart du temps pour les neurones réels.

Figure 2.23: Décalage de phase entre le champ moyen $m^{(1)}(t)$ de la population excitatrice et le champ moyen $m^{(2)}(t)$ de la population inhibitrice. La ligne continue donne l'évolution du signal $m^{(1)}(t)$. La ligne pointillée donne l'évolution du signal $m^{(2)}(t)$. Les paramètres sont $\sigma _J=1$, $d=2$, $g=8$, $\bar{\theta}^{(1)}=0$, $\sigma _\theta ^{(1)}=0$, $\bar{\theta}^{(2)}=0.5$, $\sigma _\theta ^{(2)}=0$.