




suivant: Dynamique de taille finie
monter: Régimes oscillants synchronisés
précédent: Oscillations sur le champ
Table des matières
Index
Carte de bifurcations
Comme il a été vu, le régime dynamique à la limite thermodynamique peut être décrit à l'aide de deux
indicateurs que sont le comportement dynamique du champ moyen (régime synchrone/asynchrone)
et la divergence des trajectoires (régime stabilisé/déstabilisé).
Ces indicateurs permettent de tracer deux variétés de bifurcation dans l'espace
des paramètres, l'une marquant la frontière entre le régime synchrone et le régime asynchrone
et l'autre marquant la frontière entre le régime stabilisé et le régime déstabilisé.
Quatre types de régimes dynamiques peuvent en être déduits, à savoir :
- Régime asynchrone stable. Ce régime dynamique correspond au point fixe, déjà vu sur le modèle à une population.
- Régime synchrone stable. Tous les neurones au sein d'une même population oscillent en phase, de manière périodique ou pseudo-périodique.
On parle alors d'oscillations synchronisées.
- Régime asynchrone déstabilisé. La dynamique est comparable à un processus gaussien stationnaire, comme sur le modèle à une population.
On peut parler de chaos stationnaire.
- Régime synchrone déstabilisé. La dynamique est comparable à un processus gaussien non stationnaire, à évolution périodique ou pseudo-périodique.
On parle alors de processus aléatoire cyclostationnaire, ou encore de chaos cyclostationnaire.
Avec les paramètres (
 ,
,
 ,
,
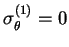 ,
,
 ,
,
 ),
les équations de champ moyen (2.6) et celles qui définissent la distance quadratique (2.7) sont itérées
pour différentes valeurs de
),
les équations de champ moyen (2.6) et celles qui définissent la distance quadratique (2.7) sont itérées
pour différentes valeurs de  et de
et de  .
Les frontières de bifurcation obtenues sont présentées figure 2.24.
.
Les frontières de bifurcation obtenues sont présentées figure 2.24.
- La ligne continue donne la transition entre les régimes stables et déstabilisés.
Pour tracer cette ligne, on fixe un
 , qui est petit (
, qui est petit (
 ),
et un temps
),
et un temps  suffisamment élevé pour atteindre le régime asymptotique (
suffisamment élevé pour atteindre le régime asymptotique ( ).
Alors, pour chaque valeur de
).
Alors, pour chaque valeur de  , on fixe une valeur initiale pour
, on fixe une valeur initiale pour  (
(
 )
et on fait croître
)
et on fait croître  avec de petits pas (
avec de petits pas (
 )
jusqu'à ce que
)
jusqu'à ce que
 ,
où
,
où 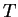 est un temps fixé qui permet d'estimer l'évolution de la
distance moyenne le long de la trajectoire (
est un temps fixé qui permet d'estimer l'évolution de la
distance moyenne le long de la trajectoire ( ).
).
- La ligne pointillée donne la transition entre la dynamique asynchrone
(
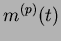 converge vers un point fixe
converge vers un point fixe
 )
et la dynamique synchrone (
)
et la dynamique synchrone (
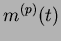 oscille pour les temps longs).
Pour déterminer cette ligne, on regarde la déstabilisation du système (2.6).
Pour chaque valeur de
oscille pour les temps longs).
Pour déterminer cette ligne, on regarde la déstabilisation du système (2.6).
Pour chaque valeur de  , on fixe une valeur initiale pour
, on fixe une valeur initiale pour  (
(
 )
et on fait croître
)
et on fait croître  avec de petits pas (
avec de petits pas (
 )
jusqu'à ce que la plus grande valeur propre de la jacobienne de (2.6)
dépasse la valeur 1.
)
jusqu'à ce que la plus grande valeur propre de la jacobienne de (2.6)
dépasse la valeur 1.
Figure 2.24:
Carte de bifurcation à la limite thermodynamique.
La carte décrit quatre régions dynamiques différentes selon  (décalage moyen) et
(décalage moyen) et  (gain), à savoir
régime de point fixe,
régime oscillant synchronisé,
régime chaotique stationnaire et
régime chaotique cyclostationnaire.
Paramètres :
(gain), à savoir
régime de point fixe,
régime oscillant synchronisé,
régime chaotique stationnaire et
régime chaotique cyclostationnaire.
Paramètres :
 ,
,
 ,
,
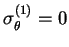 ,
,
 ,
,
 .
.
|
|
Ces quatres régions de l'espace des paramètres caractérisent les régimes dynamique du modèle
à la limite thermodynamique.
Elles étendent la gamme de régimes trouvés sur le modèle à une population.
La table 2.3 résume la terminologie employée afin de permettre
d'identifier précisément les régimes dynamiques variés observés à la
limite thermodynamique.
Tableau 2.3:
Terminologie des régimes observés à la limite thermodynamique.
| |
Asynchrone |
Synchrone |
| Stable |
Point |
Oscillations |
| |
fixe |
synchronisées |
| Déstabilisé |
Chaos |
Chaos |
| |
stationnaire |
cyclostationnaire |
|





suivant: Dynamique de taille finie
monter: Régimes oscillants synchronisés
précédent: Oscillations sur le champ
Table des matières
Index
Dauce Emmanuel
2003-05-07
 ,
,
 ,
,
![]() ,
,
 ,
,
![]() ,
,
 ,
,
![]() ),
les équations de champ moyen (2.6) et celles qui définissent la distance quadratique (2.7) sont itérées
pour différentes valeurs de
),
les équations de champ moyen (2.6) et celles qui définissent la distance quadratique (2.7) sont itérées
pour différentes valeurs de ![]() et de
et de ![]() .
Les frontières de bifurcation obtenues sont présentées figure 2.24.
.
Les frontières de bifurcation obtenues sont présentées figure 2.24.