




suivant: Discussion biologique
monter: Régimes oscillants synchronisés
précédent: Carte de bifurcations
Table des matières
Index
Dynamique de taille finie
La simulation de réseaux de taille finie permet de représenter concrètement les régimes dynamiques trouvés à la limite thermodynamique.
Toutes les simulations effectuées sur les systèmes de taille finie sont faites sur des systèmes non bruités (soit
 ).
L'absence de ce terme de bruit ne nuit pas au caractère prédictif des équations de champ moyen.
On constate en effet que les quatre régimes décrits à la limite thermodynamique se retrouvent sur les réseaux de taille finie, pour les mêmes gammes de paramètres macroscopiques,
à condition bien sûr que la taille soit choisie suffisamment grande (
).
L'absence de ce terme de bruit ne nuit pas au caractère prédictif des équations de champ moyen.
On constate en effet que les quatre régimes décrits à la limite thermodynamique se retrouvent sur les réseaux de taille finie, pour les mêmes gammes de paramètres macroscopiques,
à condition bien sûr que la taille soit choisie suffisamment grande (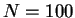 est suffisant).
est suffisant).
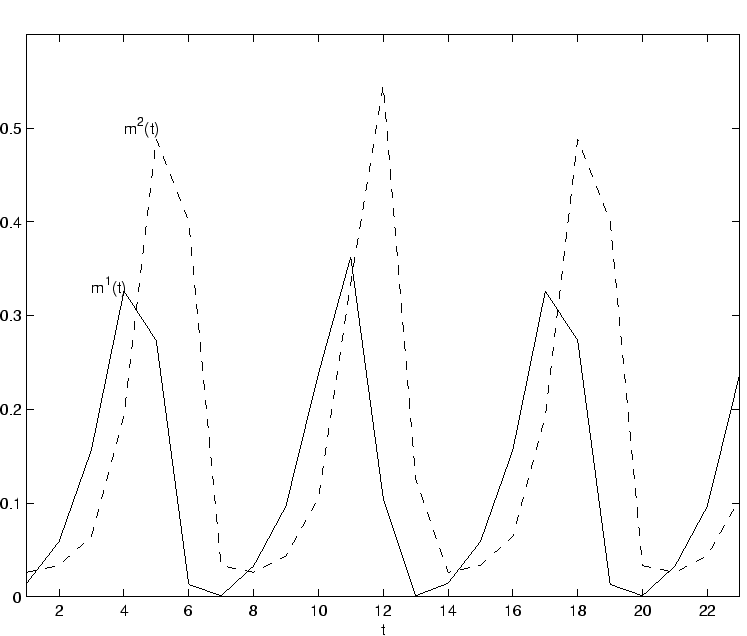
Le régime chaotique cyclostationnaire est le régime dynamique le plus nouveau par rapport au modèle à une population ; c'est celui-ci que nous décrivons sur la figure 2.25 pour un réseau de taille  .
.
On peut voir sur l'échantillon présenté que certains neurones de la population 1 tendent à avoir une activation forte au
même moment (tous les 5 pas de temps), tandis que les autres signaux d'activations restent à
une valeur proche de zéro.
Cette valeur faible en moyenne des signaux d'activation est liée à l'influence inhibitrice forte de la population 2.
Un signal fortement inhibiteur en provenance de la population 2 tend à produire des valeurs fortement négatives sur les potentiels de la population excitatrice.
Pour les neurones dont le potentiel n'est cependant pas trop négatif en moyenne, les fluctuations du signal de potentiel permettent d'atteindre la partie linéaire de la fonction de transfert (la partie centrale de la fonction de transfert).
Ces fluctuations apparaissent alors comme des impulsions sur le signal d'activation
 du diagramme de la figure 2.25.
du diagramme de la figure 2.25.
Il est important de bien distinguer ce régime des régimes chaotiques observés sur le modèle à une population.
En premier lieu, l'amplitude du signal moyen
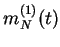 est bien supérieure à celle des signaux
est bien supérieure à celle des signaux  du modèle à une population.
L'attracteur présenté sur la figure 2.25 a un diamètre 25 fois plus important que celui qui est présenté sur la figure 2.12.
L'écart-type du signal moyen en régime synchronisé est donc très significativement supérieur à celui des régimes asynchrones, pour une même taille
du modèle à une population.
L'attracteur présenté sur la figure 2.25 a un diamètre 25 fois plus important que celui qui est présenté sur la figure 2.12.
L'écart-type du signal moyen en régime synchronisé est donc très significativement supérieur à celui des régimes asynchrones, pour une même taille  .
La seconde caractéristique spécifique de cet attracteur est la présence de cinq régions où la densité de points est plus importante.
Ces régions de forte densité sont caractéristiques de la période 5 qui est la période dominante de ce système.
Les neurones individuels tendent à atteindre leur valeur d'activation maximale tous les 5 pas de temps.
.
La seconde caractéristique spécifique de cet attracteur est la présence de cinq régions où la densité de points est plus importante.
Ces régions de forte densité sont caractéristiques de la période 5 qui est la période dominante de ce système.
Les neurones individuels tendent à atteindre leur valeur d'activation maximale tous les 5 pas de temps.





suivant: Discussion biologique
monter: Régimes oscillants synchronisés
précédent: Carte de bifurcations
Table des matières
Index
Dauce Emmanuel
2003-05-07
 ).
L'absence de ce terme de bruit ne nuit pas au caractère prédictif des équations de champ moyen.
On constate en effet que les quatre régimes décrits à la limite thermodynamique se retrouvent sur les réseaux de taille finie, pour les mêmes gammes de paramètres macroscopiques,
à condition bien sûr que la taille soit choisie suffisamment grande (
).
L'absence de ce terme de bruit ne nuit pas au caractère prédictif des équations de champ moyen.
On constate en effet que les quatre régimes décrits à la limite thermodynamique se retrouvent sur les réseaux de taille finie, pour les mêmes gammes de paramètres macroscopiques,
à condition bien sûr que la taille soit choisie suffisamment grande (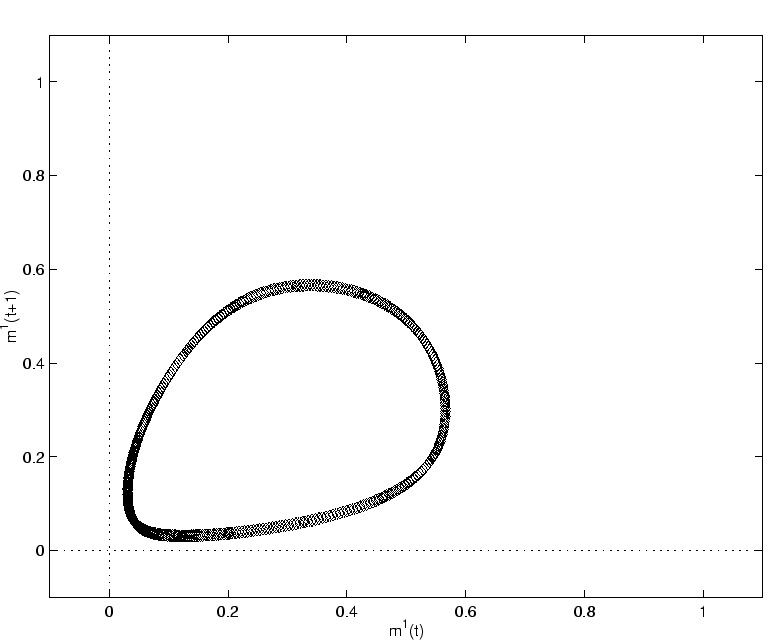 ,
,
 ,
,
![\includegraphics[]{esann_attr.eps}](img642.png)
 du diagramme de la figure
du diagramme de la figure