 et
et
Dans le cas d'une dynamique torique, une deuxième fréquence fondamentale se superpose à la première.
Ces deux fréquences  et
et ![]() peuvent être extraites du spectre de puissance.
Toutes les combinaisons
peuvent être extraites du spectre de puissance.
Toutes les combinaisons
![]() , avec
, avec
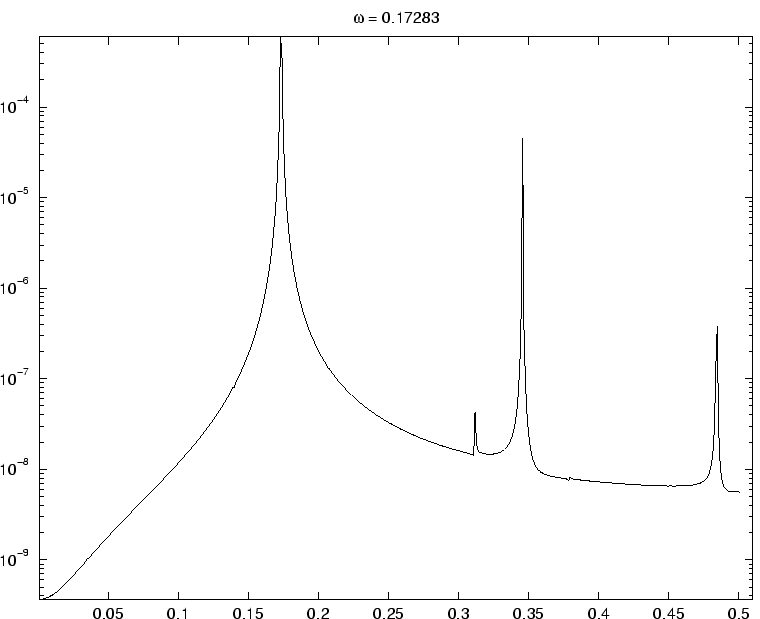
![]() , ressortent du spectre (par exemple, sur la figure 3.7, on a une fréquence qui ressort à
, ressortent du spectre (par exemple, sur la figure 3.7, on a une fréquence qui ressort à
![]() ).
Les pics correspondant à la deuxième fréquence apparue sont en général plus faibles que ceux qui correspondent à la première fréquence.
Même si dans les faits toutes ne se manifestent pas, on a par combinaison un nombre beaucoup plus important d'harmoniques, d'où l'aspect très ``hérissé'' du spectre de puissance (voir figure 3.7).
).
Les pics correspondant à la deuxième fréquence apparue sont en général plus faibles que ceux qui correspondent à la première fréquence.
Même si dans les faits toutes ne se manifestent pas, on a par combinaison un nombre beaucoup plus important d'harmoniques, d'où l'aspect très ``hérissé'' du spectre de puissance (voir figure 3.7).
|
|
Remarque : le spectre de la figure 3.7 correspond au sixième attracteur de la figure 2.10 page ![]() .
.