


Next: Discussion
Up: Robot experiment
Previous: Motor input
There are two stages in the training process. During the first 20
steps, we iterate the dynamics (1) with the forcing
motor signal, and without changing the weights, for the system to
reach its stationary dynamics. After this transient time, we
activate the learning rule (2). Due to friction between
wheels and ground, the actual rotation is slightly different from
the command issued. During the whole training process, we check
the accuracy of the angular position (we correct the position when
the shift is too big).
The learning dynamics is lasting  time steps (one time step
corresponds to one movement). This training session is not long
enough to produce a sustained feedback signal, like in previous
simulations. However, the feedback signal from layer 2 to layer 3
is stable enough to determine the motor output of the system when
the forcing signal is removed.
time steps (one time step
corresponds to one movement). This training session is not long
enough to produce a sustained feedback signal, like in previous
simulations. However, the feedback signal from layer 2 to layer 3
is stable enough to determine the motor output of the system when
the forcing signal is removed.
Figure 10:
Angular trajectories of the robot. Rotation angle versus
time. - a - Example of recalibration after a shift. The
first two steps are transients. Then the rotations issued
correspond to the learned periodic sequence
 in accordance with its associated visual
inputs (so that vision and movements are dynamically locked). Due
to friction on the ground, the real robot angle (and thus the
visual scene) shifts, leading to a progressive mismatch between
the visual scene and the movement. One can observe a sudden change
in the robot behavior (
in accordance with its associated visual
inputs (so that vision and movements are dynamically locked). Due
to friction on the ground, the real robot angle (and thus the
visual scene) shifts, leading to a progressive mismatch between
the visual scene and the movement. One can observe a sudden change
in the robot behavior (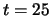 ), corresponding to an unlock between
the visual flow and the associated movements. Finally, after new
transients, the robot finds a good matching and resumes the
periodic sequence. - b - After the robot has reached its
periodic behavior, the camera is hidden. The lack of visual
information rapidly leads the robot to a "chaotic" behavior.
), corresponding to an unlock between
the visual flow and the associated movements. Finally, after new
transients, the robot finds a good matching and resumes the
periodic sequence. - b - After the robot has reached its
periodic behavior, the camera is hidden. The lack of visual
information rapidly leads the robot to a "chaotic" behavior.
|
a
b
|
After this learning process, the resulting system is tested, with
dynamics (1). The forcing motor signal is removed, so
that the robot now determines its movement according to the
feedback signal
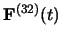 .
The robot is initially placed in an arbitrary angular direction.
Two typical angular ``trajectories'' are reported on
Fig.10.
After some transients, the robot starts to reproduce the
3-periodic sequence of rotations. This periodic movement occurs as
soon as the robot finds a matching correspondence with its visual
entries, and remains as long as visual inputs and motor commands
match together. In the first experiment (Fig.
10-a-), the reaching of the periodic behavior is
followed by a progressive shift in the robot orientation. As a
consequence, visual information progressively tends to misfit the
learned sequence of visual patterns (as the visual angle is of the
order of
.
The robot is initially placed in an arbitrary angular direction.
Two typical angular ``trajectories'' are reported on
Fig.10.
After some transients, the robot starts to reproduce the
3-periodic sequence of rotations. This periodic movement occurs as
soon as the robot finds a matching correspondence with its visual
entries, and remains as long as visual inputs and motor commands
match together. In the first experiment (Fig.
10-a-), the reaching of the periodic behavior is
followed by a progressive shift in the robot orientation. As a
consequence, visual information progressively tends to misfit the
learned sequence of visual patterns (as the visual angle is of the
order of 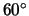 , a position misfit of the order of
, a position misfit of the order of  corresponds to an "error" of 50% in the visual field). This
increasing conflict between movement and vision leads to a
sudden change in the robot behavior. What happens is not a
take over of one movement over the other. For some time steps the
movements performed are not following the sequence anymore, nor
correspond to the ones associated with the image. After these new
transients, the robot finally finds a matching visual input,
triggers the associated movement and resumes again the good
sequence.
The movement performed by the robot in this conflict state are
still
corresponds to an "error" of 50% in the visual field). This
increasing conflict between movement and vision leads to a
sudden change in the robot behavior. What happens is not a
take over of one movement over the other. For some time steps the
movements performed are not following the sequence anymore, nor
correspond to the ones associated with the image. After these new
transients, the robot finally finds a matching visual input,
triggers the associated movement and resumes again the good
sequence.
The movement performed by the robot in this conflict state are
still  and
and 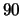 degrees rotations. There is no error
calculation between the desired rotation and the effective
rotation which could lead to other rotation angles. However,
erratic rotation and friction allow to reach visual fields that
are close enough to a learned one, so that the learned sequence of
movements can start again. In the second experiment (Fig.
10-b-)), we just hide the camera after the
robot has reached its periodic behavior. The lack of visual
information thus produces erratic rotations, and the robot keeps
searching for a matching visual input.
As we can see, our system can produce two distinct behaviors
that both depend on its visual environment and on its actual
movement. By analogy, one can interpret movements performed in the
context of dynamical systems: the change in behavior is comparable
to a phase transition from a cyclic dynamics towards a
chaotic dynamics.
degrees rotations. There is no error
calculation between the desired rotation and the effective
rotation which could lead to other rotation angles. However,
erratic rotation and friction allow to reach visual fields that
are close enough to a learned one, so that the learned sequence of
movements can start again. In the second experiment (Fig.
10-b-)), we just hide the camera after the
robot has reached its periodic behavior. The lack of visual
information thus produces erratic rotations, and the robot keeps
searching for a matching visual input.
As we can see, our system can produce two distinct behaviors
that both depend on its visual environment and on its actual
movement. By analogy, one can interpret movements performed in the
context of dynamical systems: the change in behavior is comparable
to a phase transition from a cyclic dynamics towards a
chaotic dynamics.
- The learned periodic movement corresponds to a
task associating visual inputs and motor movements. It is
stable for a broad range of visual inputs, including shifted
visual inputs.
- The "chaotic" movement can be seen as an
exploratory behavior: the search for matching visual input
sequences. When there is no possible match (for instance when the
scene is hidden, or when the robot is moved to another place), the
dynamics remains chaotic.
This preliminary experiment shows that our system can perform
reliable sensory-motor associations in a real environment
(noise on visual input, visual shifting due to the frictions on the ground...).
These associations are based on an on-line learning process, without
a priori knowledge
of the environment configuration. The secondary dynamical layer allows
the fusion of visual and motor information, and is responsible for
the stability of the control schemes, and for the dynamical adaptivity
in case of strong misfit
(the experiment is analogous
to the simulation presented on Fig.4).
It globally models the coupling between the agent and the environment in
a repetitive sensory-motor task.
In order to go further in the design of navigation systems, one
needs also to learn sensory-motor associations and environment
couplings at broader temporal scales;
- In more complex task
processing, the memory of previous behaviors may, for instance,
constrain the choice of the actual behavior, like in
Fig.6 (perseverance).
- Our model needs the repetition of a sensory-motor scheme
in order to learn it.
It is not supposed to perform
``one shot learning'' (the ability to store a
particular event in emergency conditions).
However, using the autonomous dynamics, we
could allow the system to rest, in order to store and replay
(with an inner dynamical feeding) some specific critical or
emotional sensory-motor configuration (``mental rehearsal'', see
also [34]).
- The question of learning longer
sensory-motor schemes is still open, and would
need a broader range of axonal delays for individual neurons (see
also [19] for a discussion on delays).
- The learning of non periodic behaviors
may rely on the emergence of sensory-motor schemes in a non-supervised
learning task.
Reinforcement learning methods (which relates to the pleasure or the
pain associated to some particular events) are currently under
experiment on our model, where the learning
parameters
 is a function of some
external reinforcement.
is a function of some
external reinforcement.



Next: Discussion
Up: Robot experiment
Previous: Motor input
Dauce Emmanuel
2003-04-08
![\includegraphics[width=8cm]{traj_recalage.eps}](img202.png)
![\includegraphics[width=8cm]{traj_masquage.eps}](img203.png)
![\includegraphics[width=8cm]{traj_recalage.eps}](img202.png)
![\includegraphics[width=8cm]{traj_masquage.eps}](img203.png)