... etc...)¹

A ce stade, le terme « environnement » se réfère à une source de valeurs parfaitement indépendantes du système lui-même. Nous verrons plus loin que le terme « environnement » peut également se référer à une source de stimuli agissant sur un agent (vu comme un système dynamique), mais également soumise aux actions de l'agent. Dans ce cas, la source de stimuli n'est plus indépendante de l'agent et il est nécessaire d'étendre le système à l'ensemble agent+environnement.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...autonome²

L'autonomie d'un système vivant (ou social) est classiquement définie comme la propriété du système à évoluer selon une loi propre, à s'auto-déterminer. Cette définition entre en concurrence avec la définition stricte de l'autonomie que nous donnons ici. Dans la suite de l'ouvrage, l'une ou l'autre des significations pourra être utilisées, selon le contexte. Ainsi, on parlera fréquemment de « robotique autonome », en faisant référence à la capacité du robot à construire ses propres règles, en interaction avec un environnement.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... autonome³

Un système non autonome sera défini par une fonction de transition dépendant du temps, soit $\frac{d\mathbf{x}(t)}{dt}=h(\mathbf{x}(t),t)$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

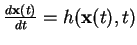... continu⁴

La discrétisation la plus élémentaire est obtenue avec le premier terme du développement de Taylor (schéma d'intégration d'Euler) :

$$\mathbf{x}(t+\Delta t)\simeq \mathbf{x}(t)+ h(\mathbf{x}(t))\Delta t$$

ce qui donne un système discret décrit par l'application $f(x)=x+h(x)\Delta t$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

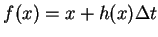... dissipatif⁵

Système qui « dépense de l'énergie » au cours du temps. Les systèmes dynamiques que nous considérons dans ce volume sont des systèmes dissipatifs.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Lyapunov⁶

Dans le cas d'un système à une seule variable réelle 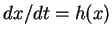$dx/dt=h(x)$, on peut définir $H(x)=-\int h(x)dx$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

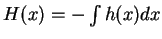... d'état⁷

au moins trois variables d'état pour les systèmes à temps continu, comme le système de Lorenz par exemple, et une seule pour les systèmes à temps discret, comme la fonction logistique.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... contrôle⁸

D'ailleurs, le projet cybernétique consistait à naturaliser les processus psychiques avec pour fondements les seules lois de la physique [DupuyDupuy1999]

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... l'agent⁹

Selon cette approche, qu'on peut qualifier de phénoménologique, on met l'environnement « entre parenthèses ».

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... tel¹⁰

Soit il s'agit de l'environnement réel pour un agent robotique, soit il s'agit d'un modèle d'environnement simulé informatiquement, qui sert de source de signaux venant « frapper » l'agent.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... « descendante »¹¹

«top down » en anglais.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... « ascendante »¹²

«bottom up » en anglais.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... émergence¹³

Est-ce un défaut d'analyse du concepteur ou est-ce radicalement nouveau, créé sur place?

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.